Mean, Variance, & Standard Deviation:
The three main measures in quantitative statistics are the mean, variance and standard deviation. These measures form the basis of any statistical analysis.
- Mean:
- Technically, the mean (denoted μ), can be viewed as the most common value (the outcome) you would expect from a measurement (the event) performed repeatedly. It has the same units as each individual measurement value.
- Variance:
- The variance (denoted σ2) represents the spread (the dispersion) of the repeated measurements either side of the mean. As the notation implies, the units of the variance are the square of the units of the mean value. The greater the variance, the greater the probability that any given measurement will have a value noticeably different from the mean.
- Standard deviation:
- The standard deviation (denoted σ) also provides a measure of the spread of repeated measurements either side of the mean. An advantage of the standard deviation over the variance is that its units are the same as those of the measurement. The standard deviation also allows you to determine how many significant figures are appropriate when reporting a mean value.
It is also important to differentiate between the population mean,
μ, and the sample mean, 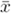 .
.
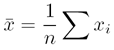
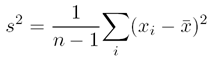

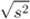 .
The advantage of using standard deviation over variance for
describing your results is that s has the same
units as the mean value.
.
The advantage of using standard deviation over variance for
describing your results is that s has the same
units as the mean value.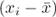 before calculating s2 and s.
Compare your standard deviation and variance with those
calculated using the built-in
before calculating s2 and s.
Compare your standard deviation and variance with those
calculated using the built-in