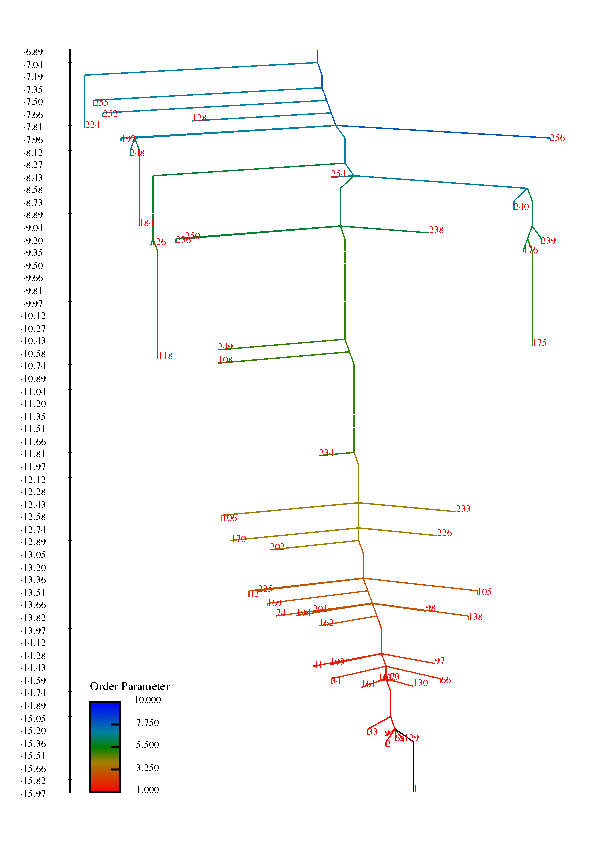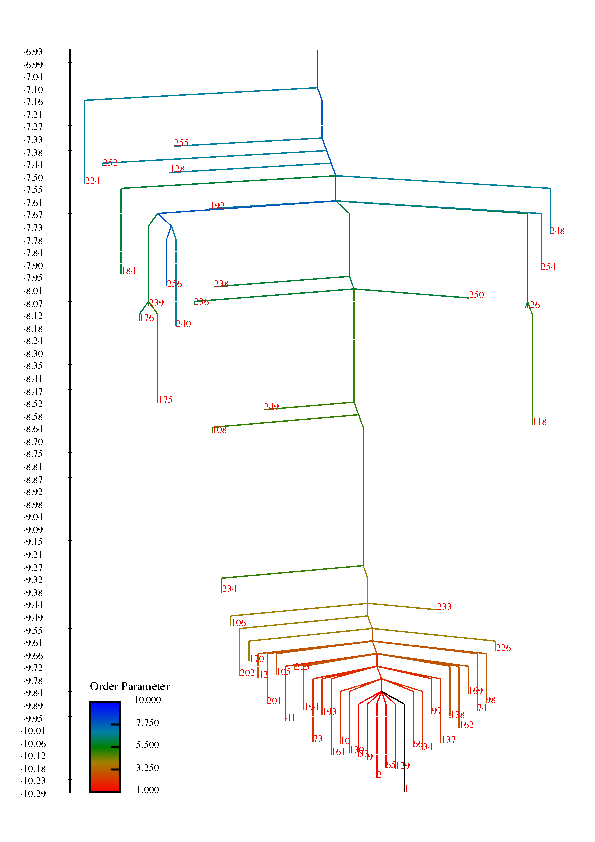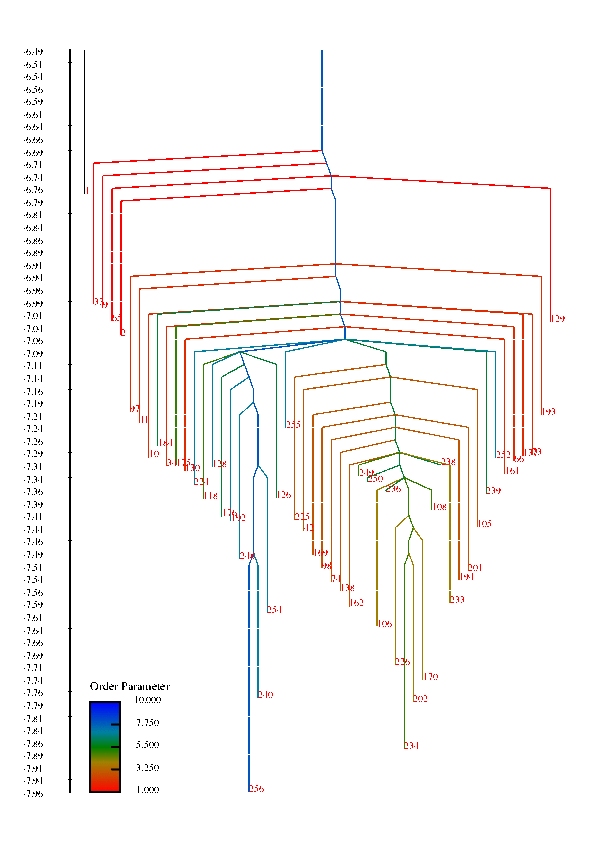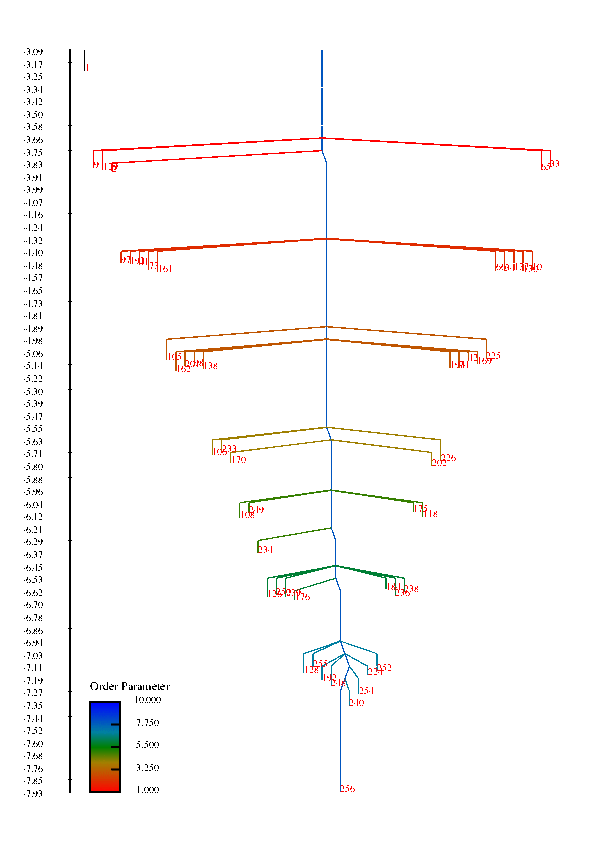
In protein chains, the competition between energy (or enthalpy) and entropy (energy density of conformational states) leads to transitions between denatured, non-native configurations and compact folded structures that play a specific function in biological systems. These competing interactions can also give rise to a wealth of other structural transitions among meta-stable states. This project is concerned with understanding the factors that influence the rate of conformational transitions and how the temperature behavior of the rates and the folding profile relate to features of the free energy surface, such as funnels. The high-dimensionality free energy surface can be viewed using disconnectivity graphs that are constructed using the free energy minima of states and estimated rates of transitions among them. In these graphs, funnels are represented in the graph by large, separated branches of states that connect only at larges values of the free energy.

This disconnectivity graph shows how the free energy landscape changes as the temperature is lowered. At high temperatures, the system is unfolded (dominant state is state 1, in black) and has a relatively high energy as well as a high configurational entropy. As the temperature decreases, the lower energy states that have lower configurational entropy become more probable, as is seen by the dropping of the folded blue state (number 256). At the folding transition temperature, the folded (blue state, 256) and the unfolded state are equally probable but in separate funnels with a significant free energy between them. At the lowest temperatures, only a single funnel exists, indicating a lack of frustration, and the folded state alone dominates.

The use of a discontinuous model of residue interactions has characteristics that may be exploited to probe the connection between the free energy surface and the folding dynamics. The interactions, tailored to produce secondary structural elements observed in real proteins such as alpha-helices and beta-sheets, may be used to unambiguously define conformations of the protein and permit temperature-independent entropic differences between states to be computed thereby allowing the free energies of all states to be computed at any temperature. Furthermore, if monomers in the protein-like chain experience rapid collisions with an effective solvent that leads to rapid decay of bead velocity autocorrelation functions, monomer dynamics may be described by the Smoluchowski equation. From the Smoluchowski equation, projection operator methods can be used to define expressions for transition rates between configurations in a Markov limit where bead correlations are short-lived on the time scale of transitions between states. Under conditions in which bead correlations are short-lived on the time scale of transitions between states, rate constants can be calculated from spectral analysis of a projected Smoluchowski evolution operator in terms of temperature-independent, one-dimensional integrals of probability densities for bonding distances that can be constructed using analytical fits to estimated cumulative distribution functions. The cumulative distribution functions and relative entropies for bonding can be efficiently computed using parallel tempering algorithms adapted to preferentially sample connected states that differ by a single bond to minimize statistical uncertainties of the computed rates. The forward and reverse rate constants for transitions between states can be expressed as a temperature-dependent linear combination of two effective rates that are temperature independent.

Although the resulting system of equations is equivalent to Markov models of proteins with continuous interaction potentials, here the Markov model is actually constructed from a physical system. Furthermore, unlike in standard systems, the discontinuous interaction potentials enable configurations to be identified without resorting to carrying out simulations and allow the computation of rate constants at any temperature. The resulting linear system can be readily solved to characterize the relaxation profile of an ensemble of unfolded configurations to the folded state as a function of temperature. The multi-exponential nature of the profile can be characterized by looking at the relative weights of eigenvectors of the linear system to distinguish between stretched and compressed-exponential kinetics. Pathways of relaxation and trapping states can be identified from the transition matrix of the Markov model to identify common features of folding trajectories.

The Schofield group is working towards developing discontinuous potential models of protein-like chains by treating some of the system, such as alpha-helices, as rigid objects that are linked together by flexible regions of the system. The interactions of residues and fragments can be constructed using discretizations of continuous potential interactions, while the dynamics of the rigid fragments can simulated using rigid body discontinuous molecular dynamics. By eliminating small-scale motions of rigid components of the biomolecule, one can focus on important motions of domains of the protein system at long times, such as hinge-bending, partial-refolding or shear domain motion.

Specific questions that will be addressed in this project include: How does the overall complexity of the connectivity map of available states influence the multi-exponential relaxation to the equilibrium population? What is the range of validity of the expressions for the rate constants? When are non-Markovian effects important? To what extent are motions in the folding process of proteins diffusive? What are the common features of folding pathways, and how are these features related to frustration in the system and the presence of secondary structural motifs?

• Movie of discontinuous molecular dynamics of 25-bead chain (5 MB)

Relevant publications

• J. Schofield and H. Bayat, "Derivation of a Markov state model of the dynamics of a protein-like chain immersed in an implicit solvent" , J. Chem. Phys. 141, 095101 (2014) (19 pages)
  
• H. Bayat Movahed, R. van Zon and J. Schofield, "Free energy landscape of protein-like chains with discontinuous potentials" , J. Chem. Phys. 136, 245103 (2012) (13 pages)
  
• L. Hernandez de la Pena, R. van Zon, J. Schofield and S. Opps, "Discontinuous molecular dynamics for semi-flexible and rigid bodies" , J. Chem. Phys. 126, 074105 (2007), (13 pages)
  
• L. Hernandez de la Pena, R. van Zon, J. Schofield and S. Opps, "Discontinuous molecular dynamics for rigid bodies: Applications" , J. Chem. Phys. 126, 074106 (2007), (12 pages)