One– and Two–Tailed Tests:
So far, we have talked in general terms about the null and alternate hypotheses without getting into the specifics of the type of comparison that we wish to make in our tests. There are two main questions we might be asking when performing our tests:
- Is our result greater (or less than) a certain value?
- Is our result within (or outside) a certain range of values?
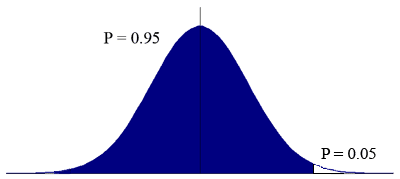
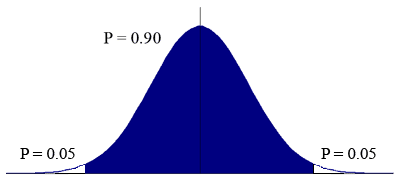
The first of these is what is known as a one–tailed test, while the second is known as a two–tailed test. This refers back to the normal distribution and our sample mean and standard deviation. Most analytical chemistry texts will present statistical tables for the various statistical significance tests in the most commonly used form for that test. On this page, you will learn the difference between one– and two–tailed tests, and what to do if the table you have isn't for the form that you need.