Degrees of Freedom:
When we discussed the calculation of the variance and standard deviation of a sample population, we used the formula:
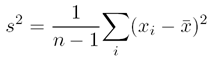
At the time, we said that we used the term (n − 1) in the denominator since it was impossible to estimate the spread of replicate results if you only had one of them. In other words, to calculate s or s2, we need at least n = 2 values.
This is an illustration of the more general concept in statistics of degrees of freedom (d.o.f. or, more simply, ν). Essentially, if we wish to model the population variance (σ2) or standard deviation (s2) from the spread of the data, we need ν = (n − 1) degrees of freedom.
Variance is a single-parameter model of the behaviour of the system under study. More complex models have more parameters. A linear model of a system, for example, requires both the slope and intercept of the straight line modelling the system to be calculated. In this case, there are two parameters to the model, so we require ν = (n − 2) degrees of freedom. This makes sense, because in order to determine if data pairs lie on a straight line, you must have at least three; any two points can always be connected by a straight line, but that doesn't mean that the relationship between them is linear!
In general, if a model requires k parameters, then the number of degrees of freedom is:
ν = (n − k)
Another way of putting this is to say that for any given statistical model, we need at least (k + 1) data points before we can fit it.
Continue with Linear Regression...